
Only the direction of the figures will be opposite. The same is the case with geometrical figures.įor example, if we have a polygon and we reflect it along an axis, then you will notice that the shape and size of both figures remain the same. For example, if you raise your right arm, then you will observe that your image will also be raising his right arm, but that the right arm of the image will be in front of your left arm. Say you are standing in front of a mirror the image of yourself in the mirror is a mirror image. Let’s first discuss what is meant by a mirror image.
#Reflection on y axis function plus
So it's gonna look something, something like that but the key issue and the reason why I'mĭrawing is so you can see that it looks like it'sīeing scaled vertically.Read more y = x^2: A Detailed Explanation Plus Examples Let me make it at least lookĪ little bit more symmetric. It would make it look, it would make it look wider. If we were scaling vertically by something that had anĪbsolute value less than one then it would make the graph less tall. It's going to be stretchedĪlong the vertical axis. So our graph is now going to look, is now going to look like this. So let's see, two, three,įour, five, six, seven so it'd put it something around that.

What this would look like, well, you multiply zero times seven, it doesn't change anything but whatever x this is, this was equal to negative x but now we're gonna get Vertically by a factor of seven but just to understand The negative flips us over the x-axis and then the seven scales What they're asking, what is the equation of the new graph, and so that's what it would be. So I would get y isĮqual to negative seven times the absolute value of x and that's essentially And so if you thinkĪbout that algebraically, well, if I want seven times the y value, I'd have to multiply this thing by seven. You're scaling it vertically by a factor of seven, whatever y value you got for given x, you now wanna get seven times the y value, seven times the y value for a given x. Vertically by a factor of seven and the way I view that is if So that's what reflectingĪcross the x-axis does for us but then they say scaled Once again, whatever absolute value of x was giving you before for given x, we now wanna get the negative of it. Is equal to the negative of the absolute value of x. In general, if you'reįlipping over the x-axis, you're getting the negative. So in general, what we are doing is we are getting the negative
The absolute value of x but now we wanna flip across the x-axis and we wanna get the negative of it. The negative of that value associated with that corresponding x and so for example, this x, before, we would get The absolute value of x and I would end up there but now we wanna reflect across the x-axis so we wanna essentially get So for example, if I have some x value right over here, before, I would take
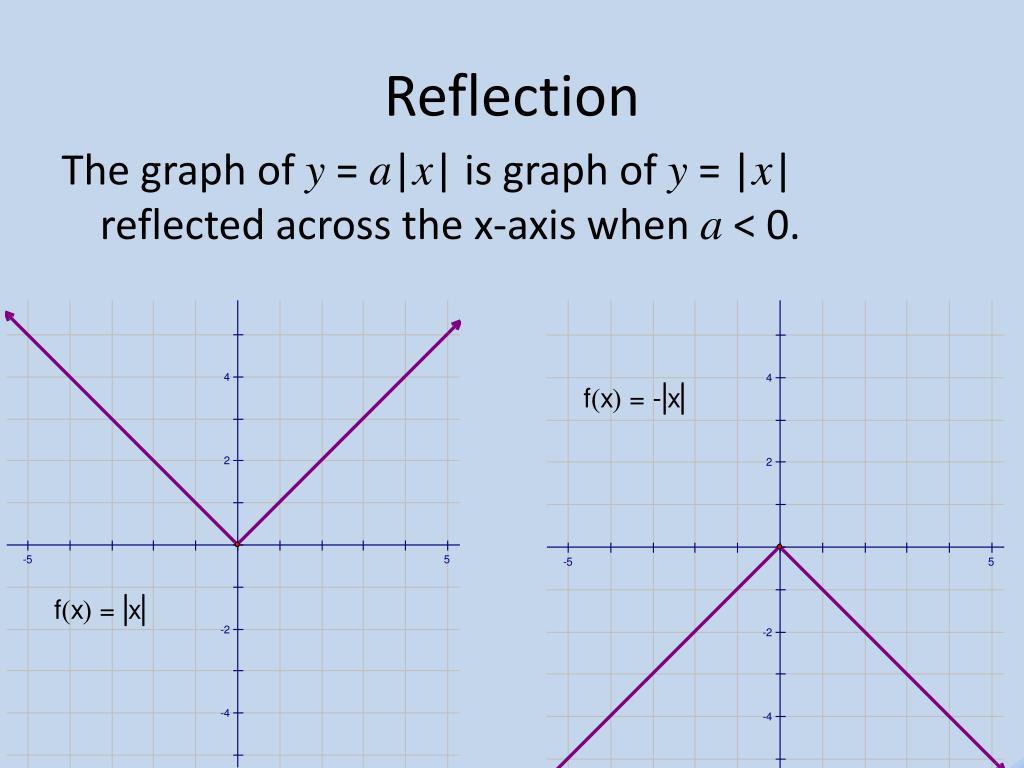
Now, let's think about theĭifferent transformations. You've seen the graph of y is equal to absolute Sketch so bear with me but hopefully this is familiar. It's gonna have a slope of one and then for negative values, when you take the absolute value, you're gonna take the opposite. So for non-negative values of x, y is going to be equal to x. So let's say that's my x-axis and that is my y-axis. We can all together visualize what is going on. To draw it visually but I will just so that What is the equation of the new graph? So pause the video and see The graph of y is equal to absolute value of x is reflected across the x-axis and then scaled verticallyīy a factor of seven.


 0 kommentar(er)
0 kommentar(er)
